Mandelbrots, Julias, and Burning Ships

Previously, in this never ending saga of fractals done in Elixir:

• The reboot of the project
• The output process
• The plan
• The minimal viable Mandelbrot
• The color schemes

My code this week is in my mandelbrot repo on Github tagged blog_2016_07_03.

This past I week I worked on implementing three more fractals. I got two of them done (i.e., I ported them from my previous Elixir program).

Random colors

But first… I forgot to include a picture of my random-coloring scheme last week:

You see more banding farther out from the set, but it gets awfully noisy close to the set. I find this useful to debug my computation and to see the overall shape, but it’s not particularly a beautiful coloring scheme.

Escape-time algorithms

As I’ve at least alluded to in the past, my program generates fractals through an escape-time algorithm applied to the points on the complex number plane¹.

Each fractal is associated with a function. For a point on the complex number plane, we repeatedly apply the function, feeding the result of one computation as input for the next.

• If the result gets too large (e.g., a magnitude greater than 2), we say that the point escapes the set; it’s outside the set.
• For any computation that lasts a certain number of iterations (e.g., 256), the original point is inside the set.

Let’s take the Mandelbrot set as an example. The formula for the Mandelbrot set is:

$$z_{n_1} = z_n^2 + c$$

To compute whether a point is in the Mandelbrot set or not, we feed it into this function as $c$, and we let $z_0 = 0+0i$, and then off we go:

$$z_0 = 0+0i$$ $$z_1 = (0+0i)^2 + c = c$$ $$z_2 = c^2 + c$$ $$z_3 = (c^2 + c)^2 + c$$

See all of that squaring? If we were dealing only with real numbers, squaring anything greater than 1 or less than 1 only makes the magnitude of $z_n$ get larger and larger. That’s boring.

Numbers between -1 and 1 stay in that range when you repeatedly square them, but that’s not particularly interesting just for real numbers.

But squaring an imaginary number is very interesting:

$$(a + bi)^2 = a^2 - b^2 + 2abi$$

It’s $-b^2$ (not $+b^2$) because we’re squaring $i = \sqrt{-1}$ along with the $b$. So the magnitude of $z_{n+1}$ might be smaller than the magnitude of $z_n$.

On the surface, this doesn’t sound to me like it’s enough to make the result interesting, and yet the Mandelbrot set proves just how interesting it can be.

So does Julia sets.

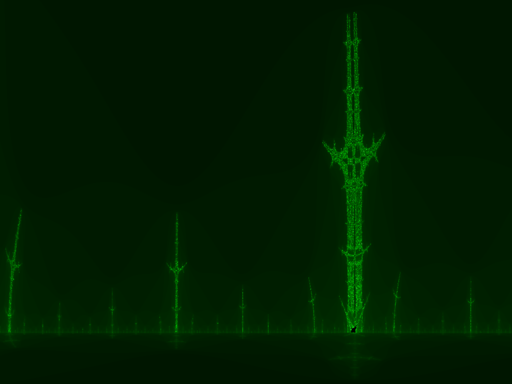
Julia sets

This is the formula for a Julia set:

$$z_n = z_{n-1}^2 + c$$

Go ahead. Scroll back a few paragraphs. It is identical to the formula for the Mandelbrot set. The difference is how we set $c$ and $z_0$.

For the Mandelbrot set, $c$ is set to the point we’re interested in, and $z_0 = 0+0i$.

For a Julia set, $c$ is a constant value for the whole set (a number we pick), and $z_0$ is the point we’re interested in. This means that there’s a different Julia set for each number on the complex number plane.

With this one change in initial parameters, we get different (but still familiar) results. Let’s see some pictures.

$c = -0.6180339887498948482045868343656381+0.0i = -\phi + 1$:

$\phi$ is the golden ratio. It comes up often in fractal discussions and images.

$c = -0.74543+0.11301i$ (some random value, I think):

The Wikipedia article has several images, and I tried reproducing them. This one turned out pretty well for me, $c = 0.285 + 0.01i$:

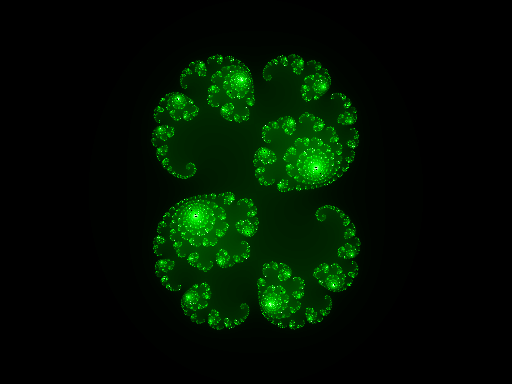
The caption on another image on Wikipedia says that it sets

$$c = (\phi - 2) + (\phi - 1)i = -0.4 + 0.6i$$

Mathematically, this is very, very wrong. $\phi$ is an irrational number—it cannot be represented as a fraction or a non-repeating decimal. Considering just the real component,

$$\phi - 2 \approx -0.381966011 \ne -0.4$$

The two approximations of $\phi - 2$ are close, but not equal, and this makes a big difference in the sets:

$c = -0.4 + 0.6i$:

$c = -0.381966011 + 0.6180339886i$:

If you compare these images to the one on Wikipedia, they must have used $c = -0.4 + 0.6i$.

The little things matter

Those last two images as approximations of $c = (\phi-2) + (\phi-1)i$ demonstrate what I find to be one of the main characters of fractals and chaos theory: a small change in your inputs can have a huge effect on the outputs. I’m a bit impressed that the two images do have the same basic outline, but the details are very different.

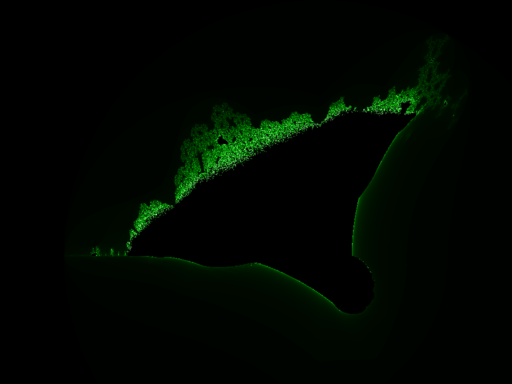
Quick! The ship is burning!

I also ported over the burning ship fractal from my previous implementation. Here’s the overall fractal²:

It looks sort of like a burning ship. No, really, it does. Its formula is actually just a simple tweak of the formula for the Mandelbrot set:

$$z_{n+1} = (|a_n| + i|b_n|)^2 + c$$

where $z_n = a_n + b_ni$ and $c$ is the point from the complex-number plane and $z_0 = 0$.

Wikipedia provides two zoomed-in pictures on the tail off to the left:

Self similar

One last interesting bit about fractals: you’ll see quite a lot of self similarity. That last zoomed-in picture of the burning ship looks a lot like the over picture. I’m certain that’s not the only place you’ll see that in the burning-ship fractal. You’ll see the same thing in the Mandelbrot set as you zoom in.

All of the Julia sets above are very self similar without zooming in. (I believe this holds true for all Julia sets.)

Ideas

It’s one thing for me to say there’s this self similarity; it’d be another if I actually proved it. Proving it with multiple pictures is rather time consuming: find the complex numbers for the corners (by hand) and enter them into a YAML file (by hand) and then generate the image (by hand). If it’s not quite right, try again. Frankly, I’d rather be programming.

I’ve been thinking about the overall architecture of my app. I started to think that maybe the Fractals application itself should be a permanent server that a user just starts once. A CLI client just connects to the one server to have its fractal generated; it may or may not wait for the image to be written. I could run multiple CLI clients at the same time, and the Fractals application would manage all of their fractals.

Then it becomes even easier to add a GUI client. It would connect to the same Fractals application, but its output would go to a window instead of a file. I’ve seen a few Elixir apps made with wxWidgets through Erlang’s wx application³, and I’ve wanted an excuse to try it out myself.

At first “GUI client” meant “another output” to me, but a true GUI client should also be interactive. And then it’s easier for both you and me to go exploring fractals to find those self-similar bits

Next week

As I said in the introduction, I started to work on three fractals. The two I got done came from the previous version of my program. The third one is completely brand new: a sinusoidal Mandelbrot set. I got the idea from “Mandelbrot Magic” a section of book on the Fractal Foundation website. They suggest iterating this:

$$z_{n+1} = z_n \sin z_n$$

It’s not quite computing the image that they say it should, and I need a little more time to figure it out.

That page also has a Nova fractal (which I don’t think is the same as the Nova fractal I implemented in Haskell) and a Magnet fractal. I’d like to try these as well.

Hopefully I can get at least one or two of these done this week.

Footnotes

elixir fractals